Skip to main content

Menemukan Formula pada Induksi Matematika (1)

Syarat: Untuk memahami contoh berikut, Anda terlebih dahulu memahami dengan jelas materi pertama pada pelajaran ini. Cek kembali postingan pada Google Kelas.

Photo by Alex Kondratiev on Unsplash

Pada Materi sebelumnya di langkah-langkah Induksi Matematika telah dijelaskan cara membuktikan suatu pernyataan yang perlu diuji kebenarannya. Pada materi tersebut Anda dituntut untuk membuktikan suatu pernyataan. Pernyataan tersebut berupa barisan bilangan tertentu dan Anda perlu membuktikan formula yang dicantumkan benar atau tidak.


Dan pada materi kali ini, Anda akan merancang suatu formula pada barisan bilangan yang telah ditentukan. Dengan Anda merancang formula barisan tersebut Anda dapat dengan mudah menentukan hasil suatu penjumlahan barisan suatu bilangan.

Pelajari dengan seksama contoh di bawah ini!!!

1.   Tanpa menggunakan alat bantu hitung, rancang formula yang memenuhi pola penjumlahan bilangan 1 hingga 20. Kemudian, uji kebenaran formula yang telah ditemukan sedemikian sehingga berlaku untuk penjumlahan bilangan mulai dari 1 hingga n, dengan n bilangan asli.

Untuk mendapatkan formulanya, maka:

a.   Selisih dua bilangan yang berurutan selalu sama yaitu 1

b.  
Hasil (1+20) = (2+19) = (3+18) = (4+17) = ………..= (10+11) = 21.

Dengan demikian, terdapat sebanyak 10 pasang bilangan yang jumlahnya sama dengan 21.

Dengan demikian, hasil dari 


10 pasang x 21 = 210. Bingung??? Perhatikan cara penulisan secara matematika berikut.

Penjelasannya adalah…..

20 adalah banyaknya n

2 adalah pembagi agar didapatkan angka 10 (10 pasang)

21 adalah hasil penjumlahan dari 10 pasang bilangan.

Masih bingung??? Parahmen.

Lanjutan dari pertanyaan pada contoh diatas adalah….

Uji kebenaran formula yang telah ditemukan sedemikian sehingga berlaku untuk penjumlahan bilangan mulai dari 1 hingga n, dengan n bilangan asli.

Jawaban

Pada jawaban di atas Anda dapat menyimpulkan sebuah formula yaitu

Oleh karena Anda telah mengetahui formula yang digunakan untuk penjumlahan barisan bilangan tersebut, maka Anda bisa menjawab dengan mudah soal berikut….

Dengan tutup mata, Anda dengan mudah menjawab soal bagian a

Apakah Anda bisa menjawab contoh soal bagian b, dan c? Tuliskan jawabanmu dikolom komentar pada postingan ini.

Download file materi ini di sini

Penjelasan lebih lanjut pada video pembelajaran berikut ini!


Labels:

Comments

  1. Fredin Samohouni ZaiAugust 9, 2021 at 10:46 PM

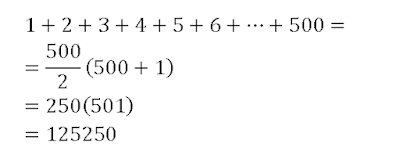
    b.1+2+3+4+5+6+...+1500=
    =1500/2(1500+1)
    =750(1501)
    =1125750

    c.1+2+3+4+5+6+...+2500=
    =2500/2(2500+1)
    =1250(2501)
    =3126250

    ReplyDelete
  2. UnknownAugust 9, 2021 at 10:52 PM

    Nama : Oktaviani Nilka Zalukhu
    Kelas : XI-MIA 1
    Jawaban :
    b. 1+2+3+4+5+6+...+1500 = 1500/2 (1500+1) = 750(1501) = 1.125.750

    c. 1+2+3+4+5+6+...+2500 = 2500/2 (2500+1) = 1250(2501) = 3.126.250

    ReplyDelete
  3. Nosta Perlin NazaraAugust 10, 2021 at 4:23 AM

    Terus semangat belajar! Kamu sudah mengerjakan dengan baik.

    ReplyDelete
  4. UnknownAugust 10, 2021 at 11:58 AM

    Nama : Vebrina Zalukhu
    Kelas : XI-MIA1
    Jawaban:
    b.1+2+3+4+5+6+...+1.500
    =1500/2 (1.500+1)
    =750(1.501)
    =1.125.750

    c.1+2+3+4+5+6+...+2.500
    =2.500 (2.500+1)
    =1.250 (2.501)
    =3.126.250

    ReplyDelete

Post a Comment

Popular posts from this blog

Analisa Saringan Agregat Halus Dan Kasar

I. Pengertian Umum Metode ini dimaksudkan sebagai pegangan dalam pemeriksaan untuk menentukan pembagian butir (gradasi) agregat halus dan agregat kasar dengan menggunakan saringan. II. Tujuan Umum Tujuan pengujian ini ialah untuk memperoleh distribusi besaran atau jumlah persentase butiran baik agregat halus maupun agregat kasar. Distribusi yang diperoleh dapat ditunjukan dalam table atau grafik. Foto oleh  Kenneth Carpina  dari  Pexels III. Peralatan Peralatan yang digunakan adalah sebagai berikut: 1.     Neraca dengan ketelitian 0,01 gram 2.     Satu set saringan;No. 4 (4.75 mm) ; No. 8(2,36 mm) ; No. 16(1,18 mm) ; No. 30(0,600 mm) ; No. 50(0,300 mm) ; No. 100(0,150 mm) ; No. 200(0,075 mm) 3.     Mesin pengguncang saringan 4.     Kuas dan alat-alat lainnya IV. Bahan Percobaan Benda uji diperoleh dari alat pemisah contoh atau cara perempat banyak : benda uji disiapkan berdasarkan standar y...
Post a Comment
Read more

Pemeriksaan Atterberg Limit Untuk Batas Plastis (Plastis Limit)

I. Pengertian Umum Batas plastis adalah kadar air minimum dimana tanah masih dalam keadaaan plastis. Tanah akan bersifat sebagai bahan yang plastis untuk kadar air yang berkisar diantara Wl dan Wp. Kisaran ini disebut indeks platisitas. Foto oleh  Anna Shvets  dari  Pexels II. Tujuan Pemeriksaan Pemeriksaan ini dimaksudkan untuk menentukan kadar air suatu tanah pada keadaan batas plastis. III. Peralatan Peralatan yang digunakan adalah : 1.     Plat kaca ukuran 30 cm x 30 cm 2.     Sendok dempul 3.     Neraca dengan ketelitian 0,01 gram 4.     Cawan kadar air 5.     Spatula 6.     Botol tempat air suling 7.     Air suling 8.     Oven yang dilengkapi pengatur suhu ( 110  ±  5 ) 0 C IV. Bahan Uji Bahan uji adalah bahan/tanah yang lewat saringan no. 40 ( 0,425 mm ). Dalam menentukan batas cair ini diperlukan 2 (dua) ...
Post a Comment
Read more